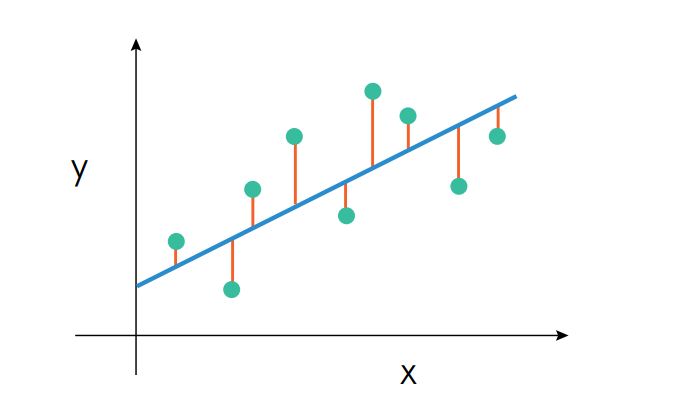
La regresión nos permite predecir uno o varios valores.

OLS

Uno de los algoritmos mas simples es el OLS. Sirve tanto para regresión simple como regresión múltiple. Consiste en una función matemática muy sencilla(combinación lineal de los atributos) del siguiente modo:

\hat{y}=W_0+W_1\cdot X_1+\cdots +W_p\cdot X_p

\hat{y} es el valor predicho, X hace referencia a los parámetros y W a los coeficientes del modelo; W_0 es el termino independiente de la combinación lineal.

Este es un proceso iterativo en el que vamos ajustando los coeficientes y por lo tanto requiere una función objetivo(función de bondad o coste)) para evaluar la bondad de una posible solución, en OLS la función se expresa como:

f(W_0,\cdots,W_p)=\frac{1}{2n}\cdot\sum_{i=1}^{n}((W_0+\sum_{j=1}^{p}W_j\cdot X_{i,j})-y_i)^2

Básicamente consiste en la suma de las diferencias al cuadrado entre la estimación del modelo(coeficientes) y la clase real. El factor \frac{1}{2n} actúa como corrección al volumen de datos de entrenamiento, con el fin de normalizar la función objetivo.

Particularidades a tener en cuenta

  • Simplicidad del modelo.
  • El modelo es fácil de interpretar. A mayor valor del coeficiente mas relevancia tiene en el modelo.
  • Gran eficacia en problemas de índole lineal.
  • Tiempo de entrenamiento muy razonable.
  • Tiempo de predicción casi instantáneo debido a que genera una única función matemática.

 

  • Se requiere variables estadísticamente independiente, sin correlación significativa.
  • Los valores se deben aproximar a una distribución normal. Los outliers afectan significativamente al modelo.
  • La homocedasticidad de los datos.

En el ejemplo a continuación se usa validación cruzada pero es innecesario por que no hay parámetros a optimizar.

En el anterior ejemplo de OLS introducimos esta métrica, y es que es exclusiva de modelos lineales. R^2 es el coeficiente de determinación y recoge la cantidad de variabilidad de la clase con respecto a su media aritmética.

R^2=1-\frac{\sum_{i=1}^{n}(y_i-\hat{y_i})^2}{\sum_{i=1}^{n}(y_i-\bar{y})^2}

\bar{y} es la media aritmética de los valores de una clase. En R^2=1 indica una predicción perfecta.

KNN (Vecinos más cercanos)

Este método se basa en la premisa de que ejemplos similares presentan un comportamiento similar en su clase, es decir que podemos agrupar por sus características. Este acercamiento nos sirve tanto para regresión como clasificación y por su algoritmo lo podemos usar tanto en aprendizaje supervisado como no supervisado.

Básicamente en aprendizaje supervisado consiste en generar como predicción el promedio de los ejemplos de entrenamiento mas parecidos a la entrada. Para encontrar los vecinos mas cercanos la clave esta en definir una distancia:

  • Minkowski(e_i,e_j)=(\sum_{d=1}^{p}|x_{i,d}-x_{j,d}|^q)^{\frac{1}{q}}
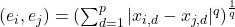
  • Euclidea(e_i,e_j)=\sqrt{\sum_{d=1}^{p}|x_{i,d}-x_{j,d}|^2}

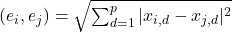
En realidad es la misma distancia y solo vamos variando el valor de la q.

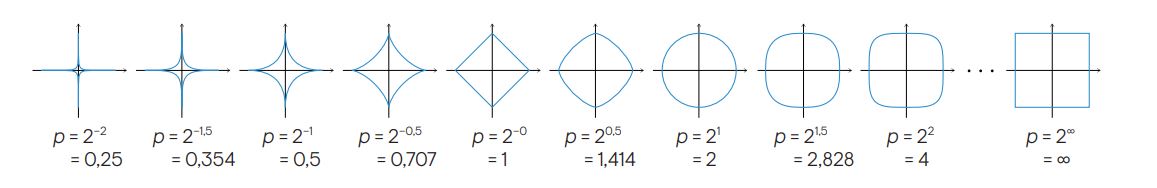
En la mayoría de los casos la distancia mas usada es la euclídea. Sin embargo independiente de la que queramos usar la distancia debe cumplir con las siguientes propiedades matemáticas:

  • No negatividad: d(e_i,e_j)\geq0
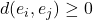
  • Identidad: d(e_i,e_j)=0\Leftrightarrow e_i=e_j
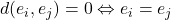
  • Simetría: d(e_i,e_j)=d(e_j,e_i)
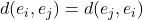
  • Desigualdad triangular: d(e_i,e_r)+d(e_r,e_j)\geqd(e_i,e_j)

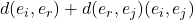
Particularidades a tener en cuenta

  • Es fundamental estandarizar los atributos, este algoritmo es muy sensible a la escala en los rangos de valores.
  • Determinar una buena función de distancia.
  • La ponderación de los vecinos, si un vecino mas cercano tiene mas peso.
  • La ponderación de los atributos, si un atributo es mas relevante que otro.
  • Simplicidad.
  • Fácil de interpretar.
  • Tiempo de entrenamiento nulo.

 

  • El tiempo de ejecución se puede ampliar dependiendo de la cantidad de datos.
  • Falta de generalización.
  • Necesidad de tener en la misma escala los datos.

OLS vs KNN