Perceptrón

Esta definición es clave para entender los conceptos matemáticos de una red neuronal. Fue creada por Frank Rosenblatt en 1957 pero debido a las limitantes técnicas no se pudo avanzar en su desarrollo. Sin embargo sus bases teóricas son las mismas.

Un perceptrón es la unidad lógica básica de una red neuronal, es decir, es una neurona. Su funcionamiento es muy sencillo.

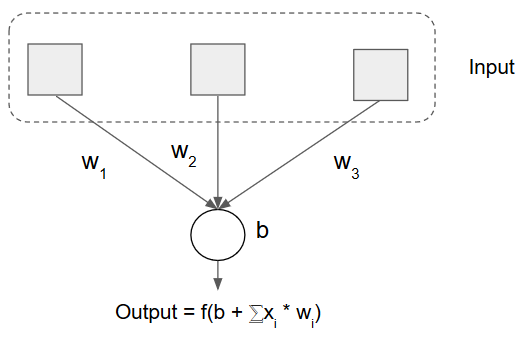
Consta de una capa de entrada(inputs) y una neurona, esta neurona procesa una función(f) de activación, donde se transforma el bias(b) + el sumatorio de las entradas-inputs(x) * los pesos(w).

La función de activación cambia dependiendo del tipo de problema que vayamos a resolver; pero eso lo veremos en otro post.

El peso se refiere a la estimulación o nivel de interacción que tendrá el input, esto quiere decir cual es la importancia de ese dato de entrada en el calculo final.

Ahora para entender el bias vamos a hacer unas representaciones de los datos y del funcionamiento del perceptrón.

Imaginemos que tenemos un sensor que registra dos datos de entrada, los cuales pueden tomar valor 1 o 0, si queremos que nuestra neurona se active con uno de los dos datos de entrada tomaría la funcionalidad de una compuerta lógica OR, si por el contrario queremos que se active cuando ambos valores son 1 funcionaria como una compuerta de tipo AND. También tenemos un caso especial con la puerta lógica XOR, es cuando queremos la activación de la neurona únicamente cuando una de las salidas es 1. Vamos a hacer sus correspondientes tablas de verdad para entender su funcionamiento.

OR

X1
X2 0 1
1 1 1
0 0 1

AND

X1
X2 0 1
1 0 1
0 0 0

XOR

X1
X2 0 1
1 1 0
0 0 1

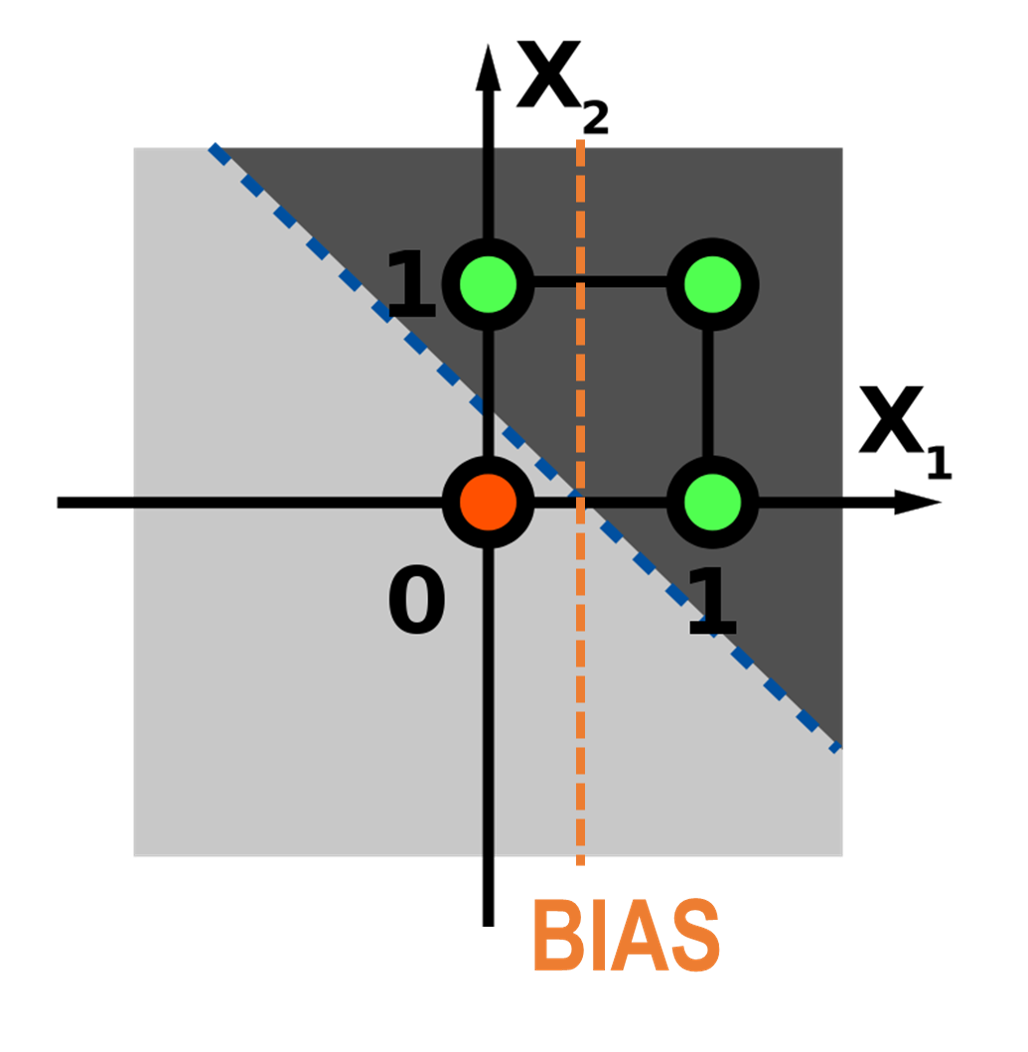
Vemos con la tabla de verdad que los datos en las compuertas lógicas OR y AND son linealmente separables, es decir, con una única línea puedo separar el espacio de valores.

El bias, corresponde justamente al valor donde se intercepta el origen y la línea de división de los datos. Este bias puede variar para restringir alguno de los espacios. Sin embargo esta definición es para una función de activación o separación lineal, estos temas los veremos mas adelante; por ahora nos quedaremos con que este valor nos ayuda a controlar la activación de la neurona.

El objetivo es ajustar los pesos y el bias para que separen los datos de la mejor manera posible. Esto lo podemos hacer en un proceso iterativo donde nos vamos acercando a los mejores valores.

En una única neurona tenemos un montón de posibles valores correctos, sin embargo como vimos, ¿que pasa con el caso de la compuerta lógica XOR? Donde necesitamos de dos líneas para separar los datos.

Perceptrón multicapa

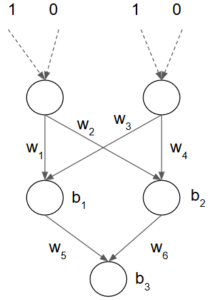
Para dar solución al problema de XOR se añade una capa oculta, es decir una línea nueva de neuronas antes de la neurona de salida, estas se encargaran de procesar los valores de los inputs para luego ser ponderados y procesados por la neurona de salida. Básicamente esta es la definición de un perceptrón multicapa, es decir le añadimos capas ocultas para aumentar la segmentación de los datos.

Sin embargo ahora tenemos una cuestión mas importante. Se menciono que tenemos  muchos valores que ajustar, y vemos que a medida que vamos añadiendo capas, estos valores crecen, y se debe encontrar los valores mas óptimos para la solución del problema. Vemos el paso a paso del proceso que conocemos como Entrenamiento.

Los valores que podemos modificar de manera global durante el proceso de entrenamiento los llamamos Hiperparámetros. Y los valores que modifica la propia red durante este proceso se llaman Parámetros.

Época

Anteriormente mencionamos que el proceso de entrenamiento es iterativo, es decir que lo repetimos un numero concreto de veces, que esta determinado por una función o valor de un hiperparámetro; a cada una de estas iteraciones la conocemos cómo época.

Una época esta formada por los siguientes pasos:

    1. Forward propagation
    2. Comparación con el ground truth
    3. Cálculo del error
    4. Backpropagation

Para profundizar en este y otros conceptos lo haremos en el siguiente post. Estará la explicación matemática de la selección de estos valores.