DESMITIFICANDO LOS ALGORITMOS: Calculando complejidad

Analizar el rendimiento de un algoritmo es una parte crucial de su diseño. Para ser útil, cualquier algoritmo debe cumplir las siguientes características:

1. Correcto: Un algoritmo debe generar resultados precisos y exactos. La verificación exhaustiva es esencial.

2. Comprensible: No debe ser excesivamente complicado de implementar. La facilidad de comprensión facilita su aplicación práctica.

3. Eficiente: La eficiencia es esencial para un buen algoritmo. Aunque pueda producir resultados correctos, su utilidad se ve comprometida si requiere un tiempo excesivo o una cantidad desmesurada de recursos computacionales.

El análisis de la complejidad espacial se enfoca en calcular la cantidad de memoria que un algoritmo requiere para procesar datos de entrada. Con el aumento de la informática distribuida y volúmenes crecientes de datos, este análisis se vuelve esencial. La eficiente asignación de recursos en las modernas estructuras de datos en memoria se convierte en un factor clave, especialmente en algoritmos iterativos, donde la naturaleza iterativa impacta en cómo se llenan las estructuras de datos y en los requisitos de memoria en distintas fases de ejecución.

• En las iteraciones convergentes, la complejidad espacial disminuye a medida que el algoritmo avanza, siendo desafiante en las primeras iteraciones.
• En las divergentes, la complejidad aumenta, y se deben establecer límites para evitar la inestabilidad.
• En las iteraciones planas, la complejidad espacial permanece constante.

Para calcular la complejidad espacial, se enfoca en las iteraciones más complejas, generalmente las iniciales, estimando el uso total de memoria, incluyendo estructuras de datos temporales, ejecución y valores de entrada. Este enfoque proporciona una buena estimación de la complejidad espacial del algoritmo.

Las siguientes son pautas para minimizar la complejidad espacial:

El análisis de la complejidad temporal estima cuánto tiempo tomará para que un algoritmo complete su tarea asignada basándose en su estructura. A diferencia de la complejidad espacial, la complejidad temporal no depende del hardware en el que se ejecutará el algoritmo, sino únicamente de su estructura. El objetivo principal del análisis de la complejidad temporal es responder a dos preguntas fundamentales:

1. ¿Este algoritmo se adaptará a una escala mayor? Debería aprovechar la infraestructura elástica moderna de entornos de computación en la nube, utilizando más CPUs, núcleos de procesamiento, GPUs y memoria disponibles.
2. ¿Cómo manejará este algoritmo conjuntos de datos más grandes? Es crucial evaluar cómo afecta el tamaño de los datos al rendimiento del algoritmo, asegurándose de que no solo sea preciso, sino que también pueda escalar eficientemente, especialmente en el contexto actual de “big data”.

Para alcanzar este objetivo, dado un problema y múltiples algoritmos, debemos determinar cuál es el más eficiente en términos de tiempo. Se pueden emplear dos enfoques básicos para calcular la complejidad temporal:

1. Enfoque de perfilado post-implementación: Se implementan diferentes algoritmos candidatos y se compara su rendimiento.
2. Enfoque teórico pre-implementación: Se aproxima matemáticamente el rendimiento de cada algoritmo antes de ejecutarlo.

La ventaja del enfoque teórico es que depende solo de la estructura del algoritmo, prescindiendo del hardware real, la pila de software seleccionada en tiempo de ejecución o el lenguaje de programación utilizado para implementar el algoritmo.

El rendimiento de un algoritmo típico depende del tipo de datos que recibe como entrada. Para abordar esta dependencia, se analizan distintos casos en el análisis de rendimiento:

1. Mejor caso: Considera el escenario donde los datos de entrada están organizados de manera que el algoritmo ofrece su mejor rendimiento. Proporciona un límite superior de rendimiento.

2. Peor caso: Estima el tiempo máximo que tomará realizar la tarea bajo condiciones específicas. Útil para garantizar un rendimiento mínimo en cualquier situación. Proporciona un límite inferior de rendimiento.

3. Caso promedio: Divide las posibles entradas en grupos, realiza análisis de rendimiento en una entrada representativa de cada grupo y calcula el promedio del rendimiento de cada grupo. El análisis del caso promedio no siempre es preciso, ya que implica considerar todas las combinaciones posibles de entradas, lo cual puede ser complicado.

La notación Big O indica el número de operaciones que procesará un algoritmo en lugar de mostrar el tiempo exacto de ejecución. Su objetivo es mostrar la tasa de crecimiento de un algoritmo y facilitar la comparación con otros algoritmos en términos de eficiencia.

Reglas para la notación Big-O:

1. La complejidad de un bucle en un algoritmo, que realiza una secuencia de pasos 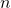veces, es .

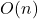2. Para bucles anidados, si un algoritmo realiza una función con un bucle de 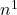pasos y, para cada bucle, realiza otro de 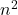pasos, la complejidad total del algoritmo es .

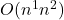3. Si un algoritmo realiza una función 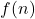que toma 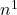pasos y luego realiza otra función 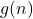que toma 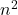pasos, la complejidad total del algoritmo es .
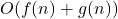4. Si un algoritmo tiene una complejidad de 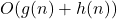y 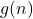es mayor que 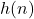para valores grandes de 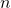, la complejidad se simplifica a .
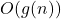   • Ejemplo: O(1+n) = O(n), y O(n2 + n3) = O(n2).
5. Al calcular la complejidad de un algoritmo, se ignoran los múltiplos constantes.

– Ejemplo: Añadir, obtener elemento, establecer elemento

Si un algoritmo tarda la misma cantidad de tiempo en ejecutarse, independientemente del tamaño de los datos de entrada, se dice que se ejecuta en tiempo constante. Tomemos el ejemplo de acceder al enésimo elemento de un array. Independientemente del tamaño del array, llevará un tiempo constante obtener los resultados.

– Ejemplo: Copiar, insertar, eliminar, iteración

Un algoritmo se considera tener una complejidad de tiempo lineal, si el tiempo de ejecución es directamente proporcional al tamaño de la entrada. Un ejemplo simple sería sumar los elementos en una estructura de datos unidimensional.

– Ejemplo: Bucles anidados

Un algoritmo se considera que se ejecuta en tiempo cuadrático si el tiempo de ejecución del algoritmo es proporcional al cuadrado del tamaño de la entrada; por ejemplo, una función simple que suma los elementos de un array bidimensional.

– Ejemplo: Encontrar un elemento en una matriz ordenada

Un algoritmo se considera que se ejecuta en tiempo logarítmico si el tiempo de ejecución es proporcional al logaritmo del tamaño de la entrada. Con cada iteración, el tamaño de la entrada disminuye por factores múltiplos constantes. Un ejemplo de un algoritmo logarítmico es la búsqueda binaria. Este algoritmo se utiliza para encontrar un elemento específico en una estructura de datos unidimensional, como en una lista en Python, siempre y cuando los elementos estén ordenados en orden descendente.

Estas son las bases matemáticas para calcular la complejidad de un algoritmo, si tienes dudas o quieres que ahondemos en alguno de estos temas, deja tu comentario. Hasta la próxima.