Números complejos
Los números complejos ![]() puede representarse como la suma de un número real y un número imaginario.
puede representarse como la suma de un número real y un número imaginario.
![]() con
con ![]()
![]()
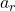 componente real,
componente real, 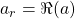
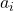 componente imaginaria,
componente imaginaria, 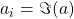
Operaciones con complejos
Suma
![]()
Producto
Recordemos que ![]()
![]()
Conjugado
El conjugado se obtiene cambiando el signo de su componente imaginaria.
![]() o
o ![]()
- La conjugación del denominador complejo juega el mismo papel que la racionalización de un denominador irracional. Se busca que el denominador sea real.
- Facilita la división de números complejos, pues al conjugar el denominador, el cociente se transforma en un producto del dividendo por el inverso multiplicativo del divisor.
- Permite calcular el módulo de cualquier número complejo.
Norma(Módulo)
Es el número real positivo que mide su tamaño y generaliza el valor absoluto de un número real. Esta noción es particularmente útil para definir una distancia en el plano complejo.
![]()
![]()
División
![]()
![]()
![]()
Forma polar
Podemos representar los números complejos como puntos en el plano, cada punto del plano se determina por una distancia y un ángulo.
Esta forma de representar los números complejos es ampliamente utilizada en física y trigonometría, ya que es normalmente mucho más simple trabajar con números complejos expresados en forma polar que con su equivalente en forma rectangular(forma que vimos anteriormente).
Formula de Euler: ![]() con
con ![]() denominada fase.
denominada fase.
Nótese que en esta fórmula, al igual que en todas aquellas en las que intervienen exponenciales de ángulos, se asume que el ángulo θ está expresado en radianes.
Veamos algunas operaciones con forma polar:
Sean ![]() , con
, con ![]()

Producto
![]()
Conjugado
![]()
División
![]()
Potencia
![]()
Exponenciación
![]()
Raíces
![]()
Hagamos unas operaciones para sacar la norma y la fase con la forma polar.
Espacio de Hilbert
Es una generalización del concepto de espacio euclídeo. Esta generalización extiende los métodos del álgebra lineal y el cálculo aplicados en el espacio euclídeo de dos dimensiones y tres dimensiones a los espacios de dimensión arbitraria, incluyendo los espacios de dimensión infinita.
El estado de un sistema cuántico viene descrito por un vector (vector de estado) en un espacio de Hilbert de componentes complejas.
Espacio vectorial complejo: conjunto no vacío de elementos, denominados vectores, que incluye las operaciones de suma, negación y multiplicación por un escalar
Los vectores se representan como arrays de 𝑛 filas y 1 columna.
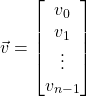
![]() y
y ![]() es la dimensión del espacio.
es la dimensión del espacio.
El espacio ![]() formado por los vectores de 2 elementos complejos con producto escalar es un espacio de Hilbert.
formado por los vectores de 2 elementos complejos con producto escalar es un espacio de Hilbert.
Notación de Dirac(bra-ket)
Es la notación estándar para describir los estados cuánticos, también se utiliza para denotar vectores abstractos y funcionales lineales en matemática.
El estado de un sistema físico se identifica con un vector en el espacio de Hilbert complejo, . Cada vector se llama un ket, y se denota como . Cada ket tiene un bra dual, escrito como , esto es una funcional lineal continua de a los números complejos C.
Ket: ![]()
Bra: ![]()
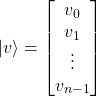
![]()
donde el símbolo ![]() representa la matriz traspuesta conjugada
representa la matriz traspuesta conjugada
Producto escalar o interno
Se utiliza para determinar si dos vectores son ortogonales.
Sean ![]() y
y ![]() vectores de dimensión
vectores de dimensión ![]() .
.
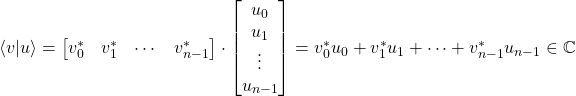
Módulo(Norma)
![]()
![]()
Esta norma es siempre positiva
![]()
Propiedades del producto interno
- Linealidad por la izquierda:-
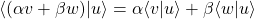 con
con 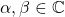
- Linealidad conjugada por la derecha:
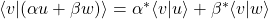 con
con 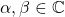
- Hermiticidad:
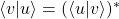
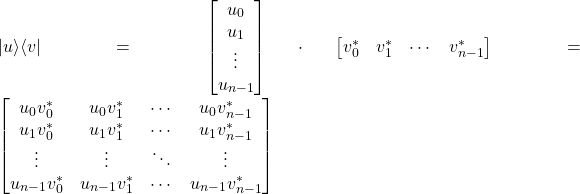
Producto externo (outer product)
Se usa para probar si dos vectores son paralelos.
El producto externo de dos vectores de dimensión ![]() es una matriz de dimensión
es una matriz de dimensión ![]()
Propiedades del producto externo
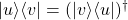
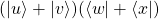
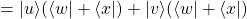
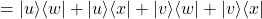
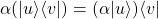
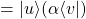 con
con 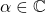
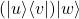
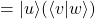
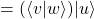 ya que
ya que 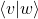 es un escalar
es un escalar
Producto tensor (Kronecker)
Denotado con
, a una operación sobre dos matrices de tamaño arbitrario que da como resultado una matriz bloque. Es un caso especial del producto tensorial. El producto de Kronecker no debería confundirse con el producto de matrices habitual, que es una operación totalmente diferente.
El producto tensor de un vector ![]() de
de ![]() elementos y un vector
elementos y un vector ![]() de
de ![]() elementos es un vector de
elementos es un vector de ![]() elementos dado por:
elementos dado por:
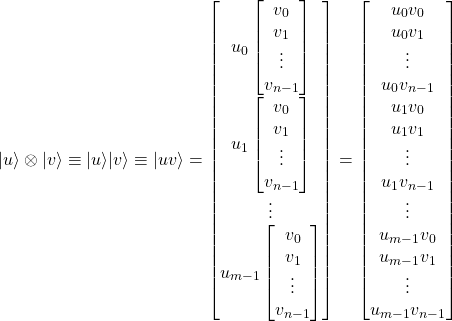
Ejemplo:
Sean, en un espacio de dimensión 2, los siguientes vectores:
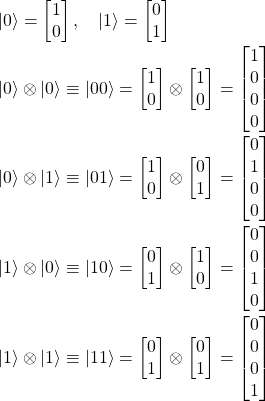
Propiedades del producto tensor
- Asociatividad y traspuesta:
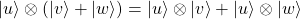
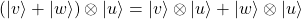
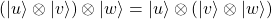
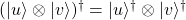
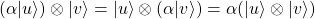 , con
, con 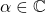
- No-conmutatividad (en general):
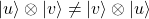
- Propiedad del producto mixto:
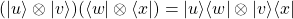
Producto tensor de espacios vectoriales
Dado un espacio vectorial ![]() de dimensión
de dimensión ![]() y otro
y otro ![]() de dimensión
de dimensión ![]() , el espacio vectorial
, el espacio vectorial ![]() tiene dimensión
tiene dimensión ![]() y se define como:
y se define como:
![]()
Base del espacio
Un conjunto de ![]() vectores es una base del espacio de dimensión
vectores es una base del espacio de dimensión ![]() si se verifica:
si se verifica:
- Cualquier vector
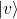 se puede escribir como una combinación lineal de los elementos de la base.
se puede escribir como una combinación lineal de los elementos de la base. - Los vectores de la base son linealmente independientes
Si, además, los vectores de la base son ortogonales (ortonormales), se dice que la base es ortogonal (ortonormal).
Ejemplo
Sean los siguientes vectores de ![]() elementos:
elementos:

es decir, el vector ![]() tiene sus
tiene sus ![]() coeficientes a 0 excepto el i-ésimo que vale 1.
coeficientes a 0 excepto el i-ésimo que vale 1.
El conjunto ![]() es una base ortonormal (llamada base canónica).
es una base ortonormal (llamada base canónica).
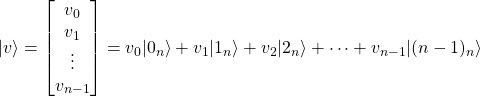
Se verifica que los vectores de la base son ortonormales, ya que:
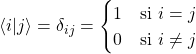
Ejemplo: cambio de base
Sea un espacio de dimensión 2. Un vector ![]() escrito en la base canónica
escrito en la base canónica ![]() queda:
queda:
![]()
Otra base es la formada por los siguientes vectores:
![]()
En esta otra base, el vector tendrá otros componentes:
![]()
Tenemos, entonces:
![]()
Es decir:
![]()
Si definimos la matriz ![]() como:
como:
![]()
es fácil comprobar que:
![]()
![]() es una matriz de cambio de base: permite obtener los coeficientes en una base a partir de los coeficientes en la otra.
es una matriz de cambio de base: permite obtener los coeficientes en una base a partir de los coeficientes en la otra.
Los vectores ![]() son ortogonales, pero no son ortonormales:
son ortogonales, pero no son ortonormales:
![]()
Para que sean ortonormales, debemos definirlos como:
![]()
y escribir la matriz ![]() como:
como:
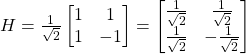
Esta matriz se denomina matriz de Hadamard, sus entradas son +1 o -1 y cuyas filas son mutuamente ortogonales.
Operadores lineales y matrices
Sea ![]() y
y ![]() espacios de dimensiones
espacios de dimensiones ![]() y
y ![]() , respectivamente.
, respectivamente.
Un operador lineal ![]() es una función que verifica:
es una función que verifica:
![]()
para todo ![]() y
y ![]()
El operador ![]() se representa mediante una matriz de dimensión
se representa mediante una matriz de dimensión ![]() y la operación
y la operación ![]() es un producto matriz-vector.
es un producto matriz-vector.
Por ejemplo, la matriz de Hadamard es un operador ![]() con
con ![]() de dimensión 2.
de dimensión 2.





Comments
Desarrolla a la Velocidad de la Luz con Qiskit: Tu Entorno Cuántico Todo en Uno - jhontona.com