Como vimos en el anterior post, a medida que vamos agregando complejidad a las operaciones necesitamos agregar capas ocultas, estas capas nos van a permitir detectar patrones y correlaciones; cada neurona se va a especializar en un patrón, es decir, se activara cuando reconozca ese patrón o relación, como una compuerta lógica.

Pero antes de continuar veamos a pequeña escala en que fundamentos matemáticos se basa para crear estos patrones y en que consiste el entrenamiento, para esto vamos a utilizar la pequeña red que habíamos mostrado para ejemplificar una compuerta de tipo XOR. Otra pequeña aclaración es que solo vamos a ver los aspectos fundamentales del entrenamiento, aclaro esto ya que a medida que avancemos vamos a ir robusteciendo estas bases agregando hiperparámetros y otros procesos a medida que sea necesarios.

Forward propagation

La propagación hacia adelante consiste en tomar los valores de entrada para validar que neuronas se activan hasta llegar a la capa de salida. Suena fácil, pero vamos a complicarlo un poquito viendo que pasa en detalle por cada una de estas capas.

Estamos muy acostumbrados a ver redes neuronales gigantes, con muchos hiperparámetros y entradas, pero claramente para aprender es mas conveniente trabajar con pocas entradas, por lo que vamos a crear nuestra pequeña red neural.

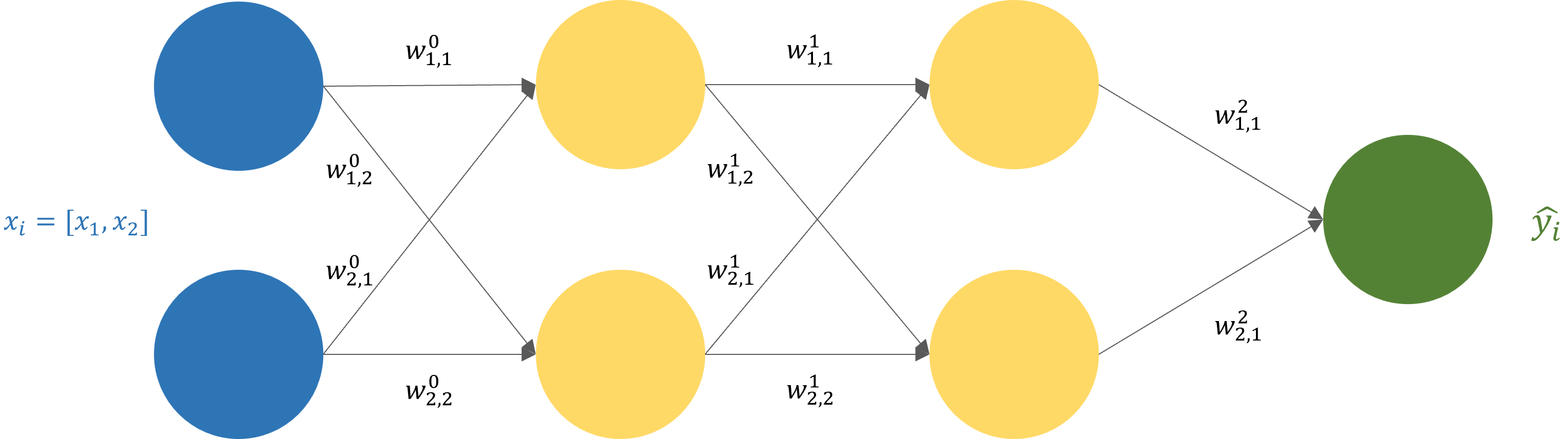
Tenemos nuestras entradas definidas por la variable x_i, estas van a interactuar con nuestras primeras neuronas, recordemos que el valor que va a llegar a la siguiente neurona esta determinado por \sum w_ix_i+b ¿De donde salen los valores para w y b? Pues en nuestra primera iteración estos valores son generados para toda la red aleatoriamente, es decir que claramente nuestra predicción \hat{y} va ser errónea, pero eso lo iremos ajustando.

Por ahora sabemos que llega un valor a nuestra neurona y esta debe decidir si se activa o no, es decir que debemos darle un umbral de decisión, aquí es donde nos apoyamos de nuestra función de activación. Una función de activación nos va a servir para determinar si el valor recibido cumple y puede continuar a la siguiente capa, a esto lo consideramos una activación.

Aquí te dejo una lista de las funciones mas usadas. Actualmente la mas utilizada es la ReLU.

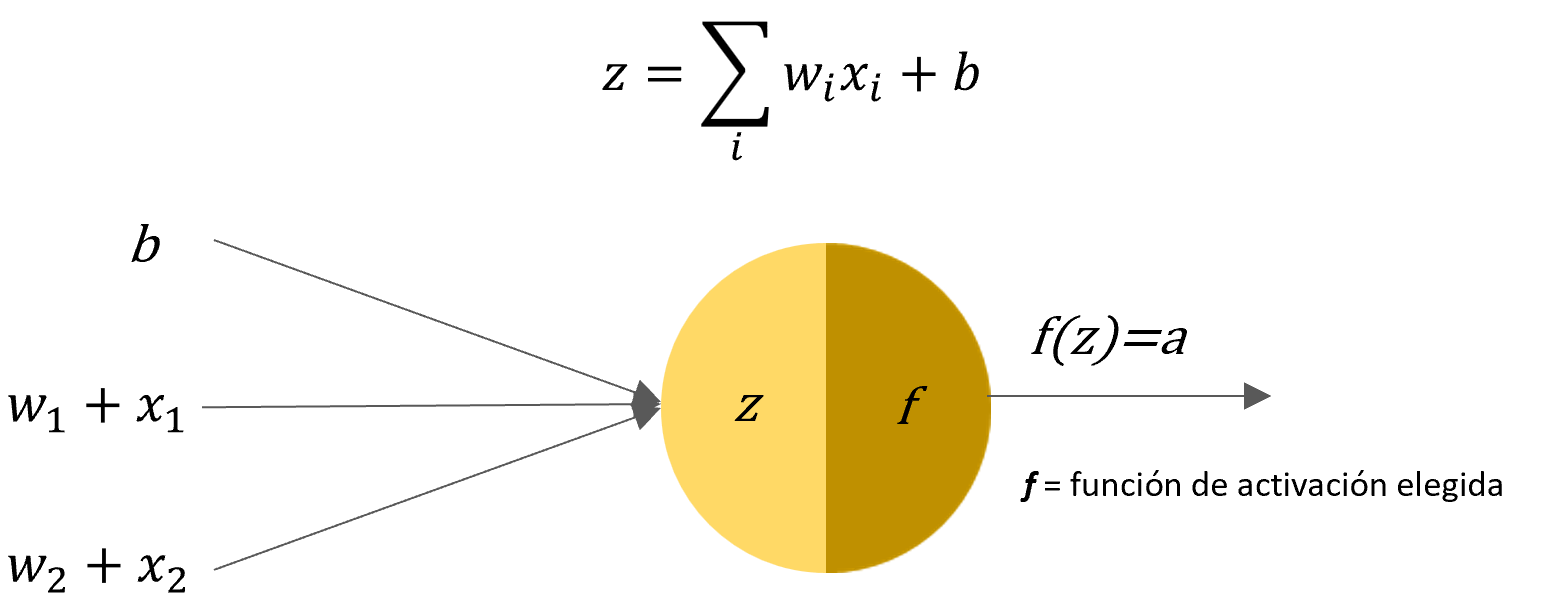
Este proceso lo vamos a hacer por cada neurona, las salidas activación de nuestras neuronas serán la entrada en nuestra siguiente capa.

En las capas ocultas lo mas probable es que tengamos funciones de activación ReLU, estas son muy comunes ya que todo lo que sea menor a 0 lo deja como 0 y estandariza el resto de valores entre 0 y 1. Sin embargo, para nuestra neurona de salida utilizamos una función de activación diferente y esto depende del tipo de problema en el que estemos trabajando. Por ejemplo, para una predicción de tipo regresión utilizamos una función linear, para un problema de clasificación usaremos la función softmax para casos de selección múltiple y la función sigmoide para clasificación binaria(una sola neurona a la salida).

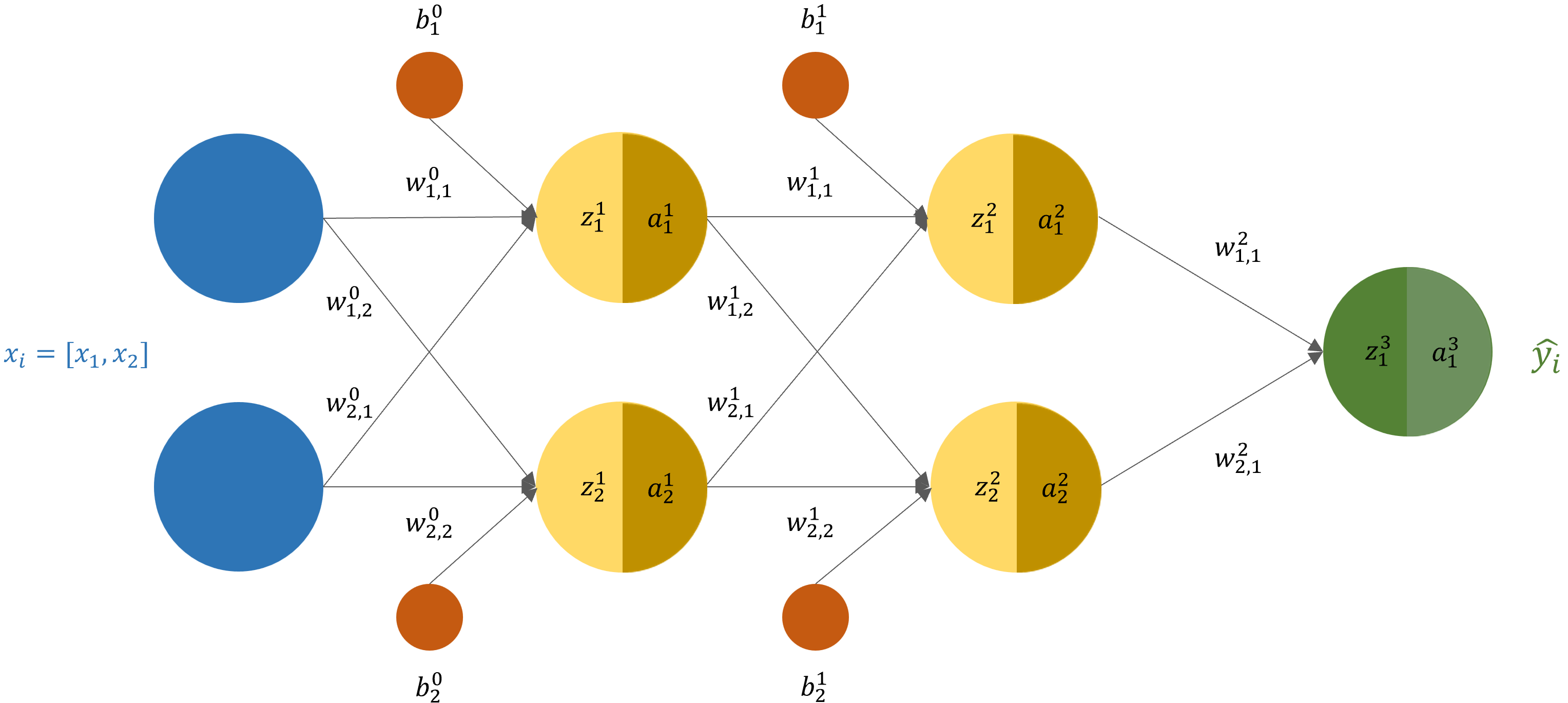
Una vez tenemos nuestra predicción \hat{y} podemos continuar con nuestro siguiente paso.

Ground truth y cálculo del error

El Ground truth hace referencia al resultado ideal esperado. Es nuestro punto de referencia para validar que tan precisas son nuestras estimaciones, por lo que inmediatamente la podemos asociar con nuestro set de datos de entrenamiento, es decir, el Ground truth esta formado por todas las mediciones de datos que se han recopilado para el entrenamiento.

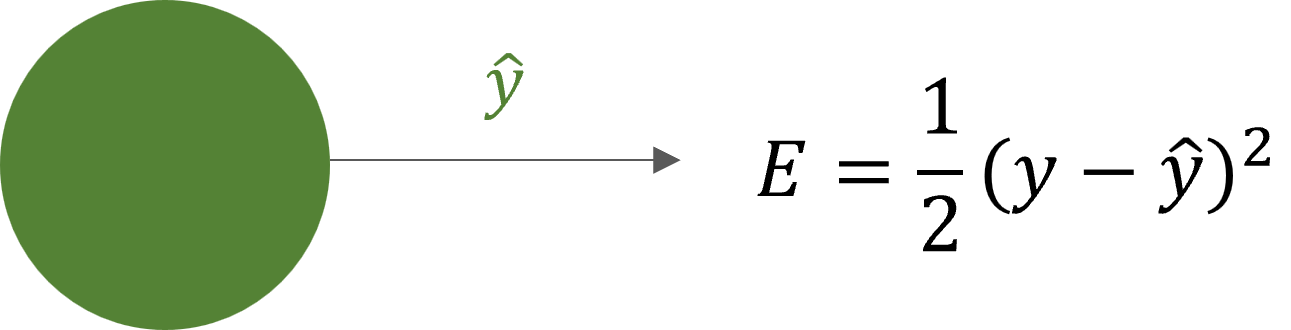
Vamos a empezar por calcular el error E, que en este caso será un medio por la diferencia al cuadrado del Ground truth y menos la predicción \hat{y}. Sin embargo recordar que tenemos diferentes opciones para calcular el error.

Backpropagation

Al iniciar el proceso se mencionó que los pesos entre neuronas se da aleatoriamente y es de esperar que el error sea alto; una vez tenemos ese error calculado debemos devolvernos y comunicar el valor del error para ajustar los pesos. El ajuste de pesos lo hacemos calculando la derivada parcial de la función aplicada, analizamos como varia el error en función de los pesos.

Tenemos que utilizar una medida de learning rate \eta (taza de aprendizaje), que me va a modular que tanto cambio los pesos, ya que la idea no es cambiarlos bruscamente si no que se dibuje una curva suave en donde se muestre como disminuye el error para alcanzar la convergencia.

Veamos como seria el calculo del nuevo peso para la primera neurona en retro propagación.

w_{1,1}^{2}(t+1)=w_{1,1}^{2}(t)-\eta \frac{\partial E}{\partial w_{1,1}^{2}}

Lo que estamos indicando es que el peso para esa neurona en nuestra siguiente iteración t, es igual peso que tiene actualmente, menos el learning rate   \eta por la variación del peso con respecto al error.

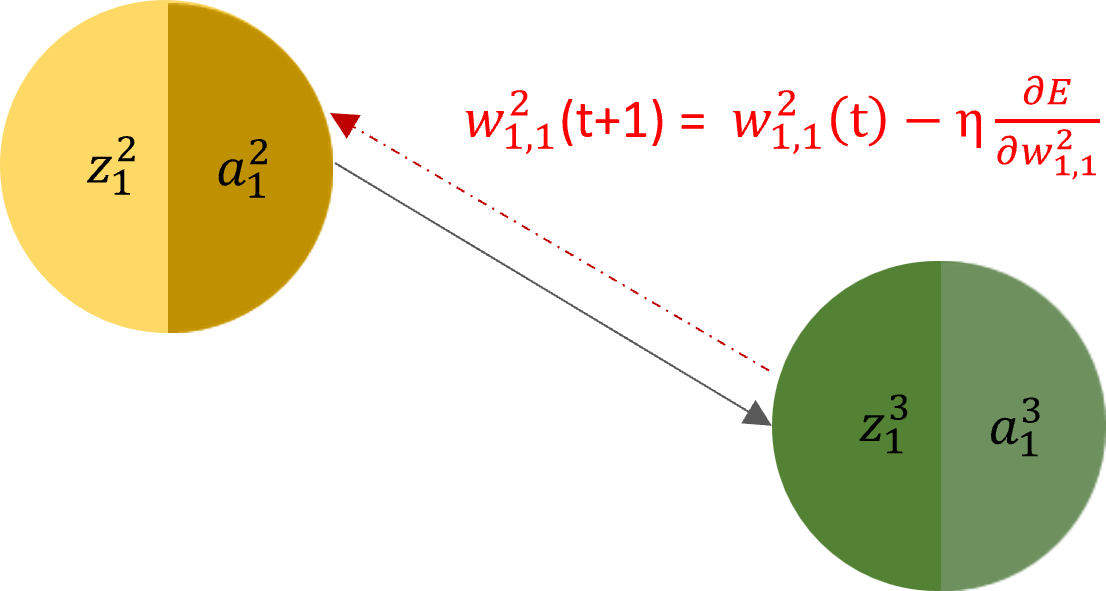
Este proceso se debe aplicar para cada uno de los pesos de la neurona, sin embargo, no se pueden calcular los pesos individualmente, ya que los pesos de una capa anterior influye en los pesos de la capa actual. Para solventar esto debemos calcular los pesos con la regla de la cadena, quedándonos la derivada de w_{1,1}^{2}(t+1) de la siguiente manera:

\frac{\partial E}{\partial w_{1,1}^{2}}=\frac{\partial E}{\partial a_{1}^{3}}\cdot \frac{{\partial a_{1}^{3}}}{\partial Z_{1}^{3}}\cdot \frac{{\partial Z_{1}^{3}}}{\partial W_{1,1}^{2}}

Finalmente podemos aplicar los cambios requeridos para ajustar cada neurona y así se repite este proceso iterativamente hasta hacer que nuestros valores deseados sean lo mas cercanos posible.

¡Conviértete en un experto tecnológico! 🚀 Suscríbete a nuestro newsletter y recibe las últimas noticias, análisis y tendencias directamente en tu bandeja de entrada. No te pierdas las actualizaciones que harán que tu experiencia tecnológica sea aún más emocionante. ¡Únete a nuestra comunidad hoy! 📧✨