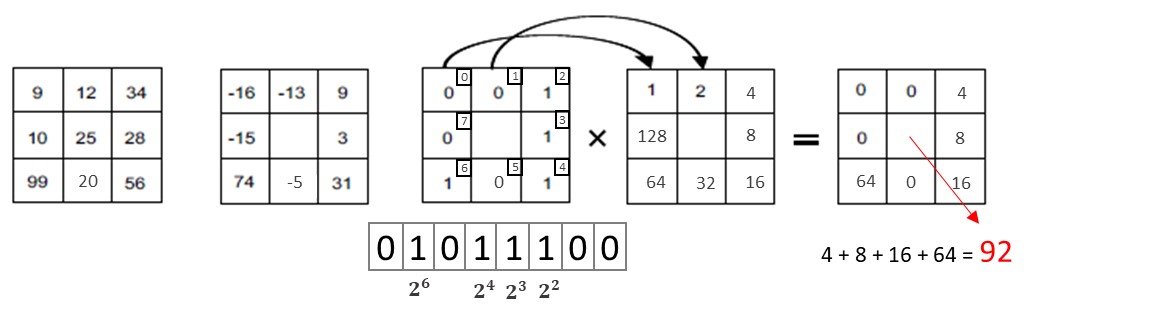
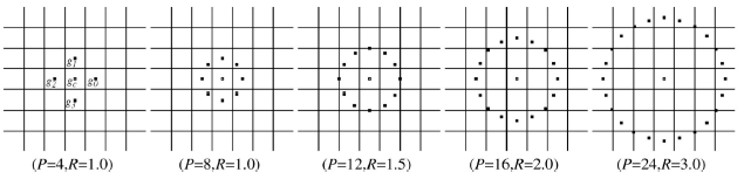
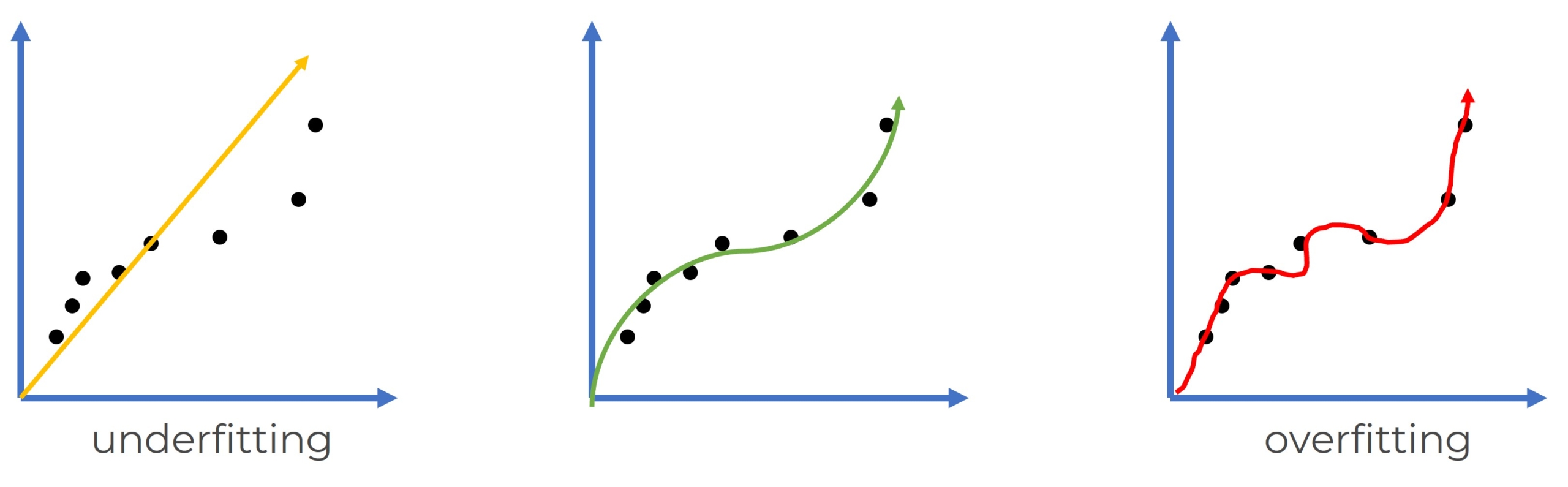
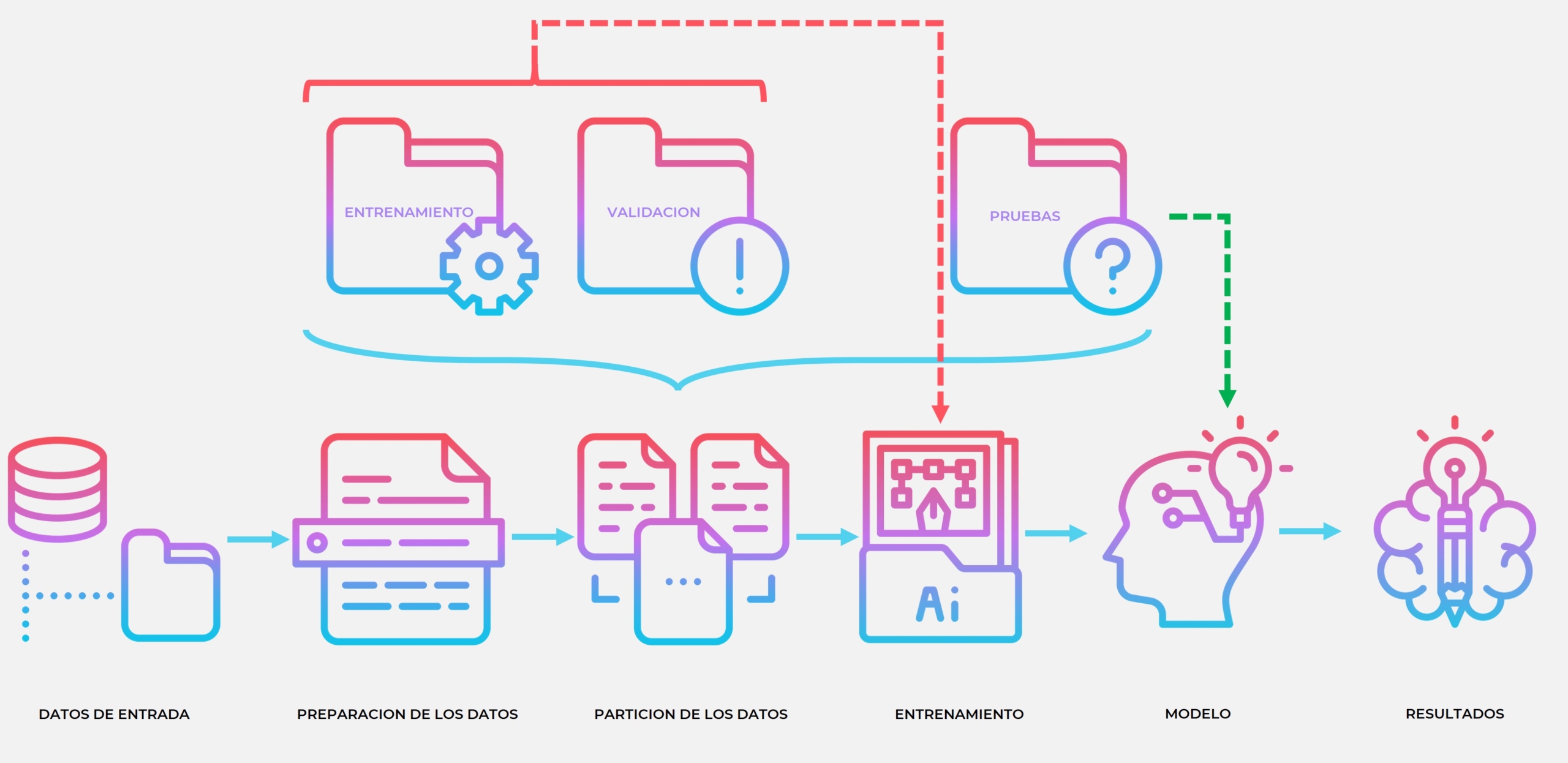
Regresión logística
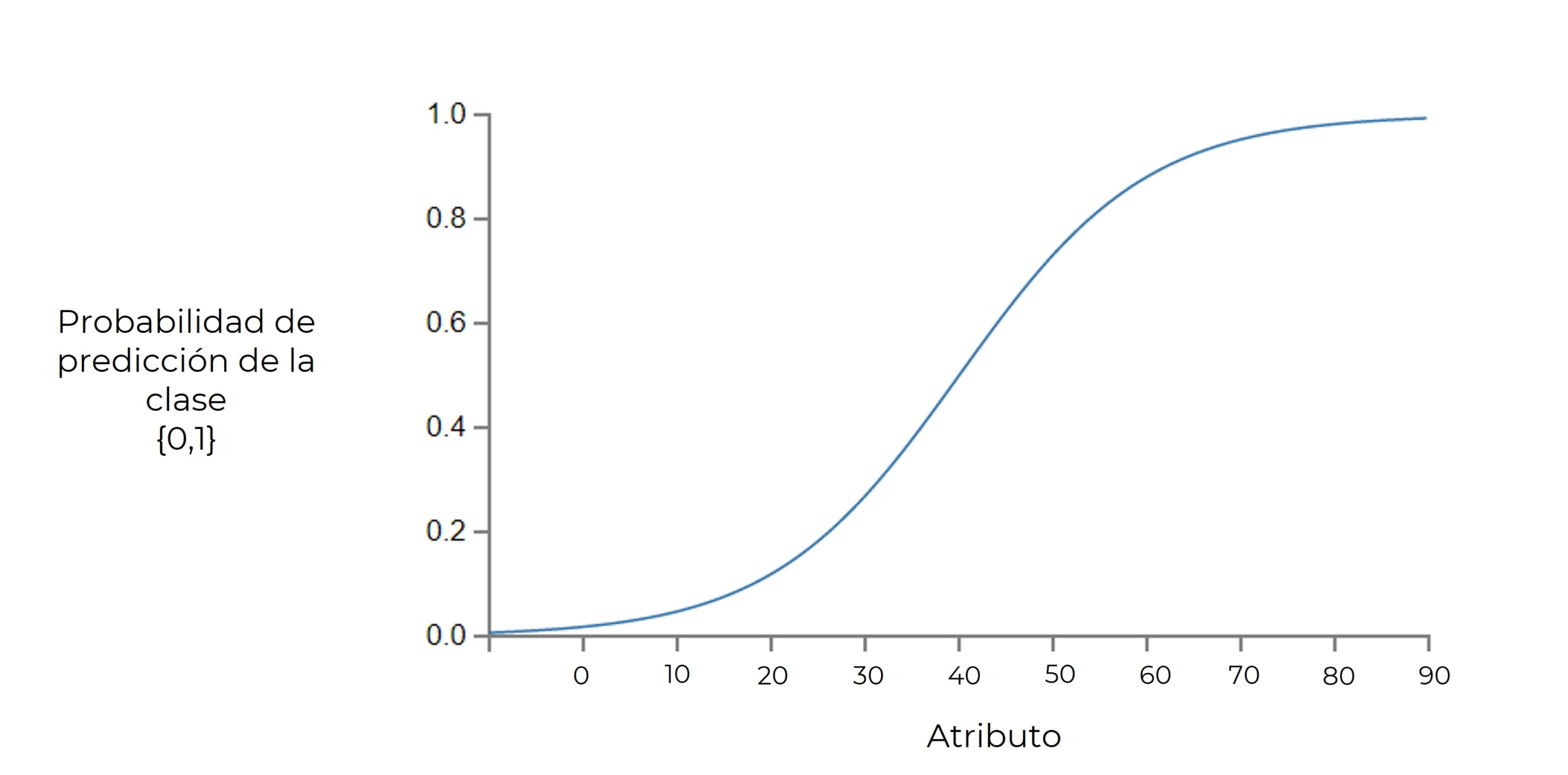
LOGR o regresión logit, a pesar de su nombre no tiene nada que ver con algoritmos de regresión, si no que es un algoritmo de clasificación. Funciona creando una frontera lineal entre dos clases, es decir que nos da una probabilidad de que la predicción pertenezca a una determinada clase, suele ser ![]() pero podemos fijar este criterio de decisión dependiendo de nuestra necesidad.
pero podemos fijar este criterio de decisión dependiendo de nuestra necesidad.
Una de las métricas mas utilizadas para medir la bondad de los clasificadores es la métrica AUC(área bajo la curva). La curva ROC mide la relación entre las tasas de aciertos y de falsos positivos en función del umbral de clasificación. Cuanto mayor sea el área bajo la curva ROC, mejor será el clasificador. Un clasificador perfecto tendrá un valor de AUC = 1.
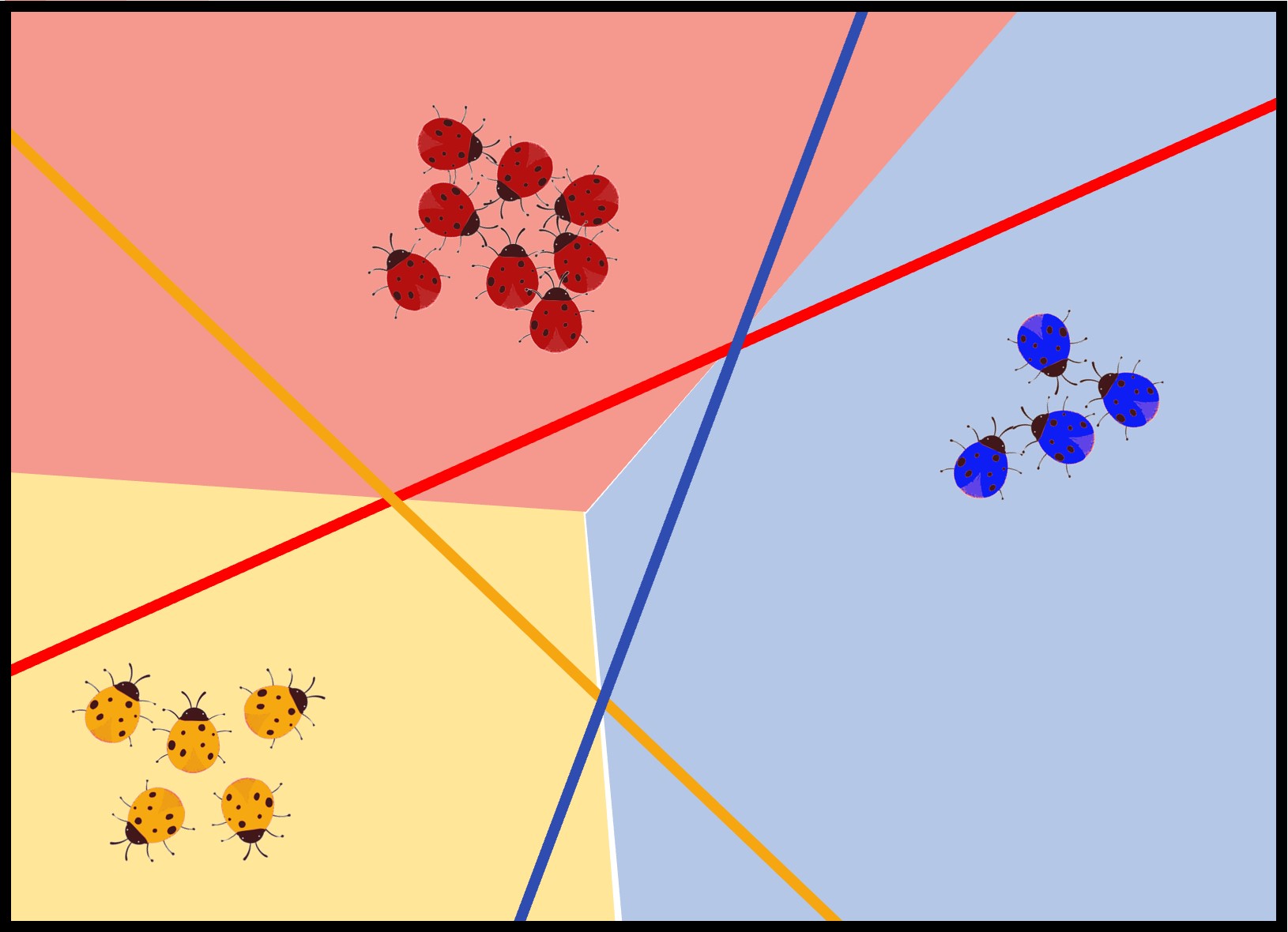
Como mencionamos anteriormente, este algoritmo separa en dos clases, es decir que cuando tenemos un problema multiclase lo que hace es validar una clase frente a todos los demás, si no corresponde toma la siguiente clase y vuelve a comparar, algo como un switch case iterativo, separa todos los items de una clase, luego la siguiente y así sucesivamente hasta que crea una línea de separación por cada clase, lo que significa que tenemos un subproblema por cada clase a predecir; con cada línea(corete de frontera) se calculan las bisectrices.
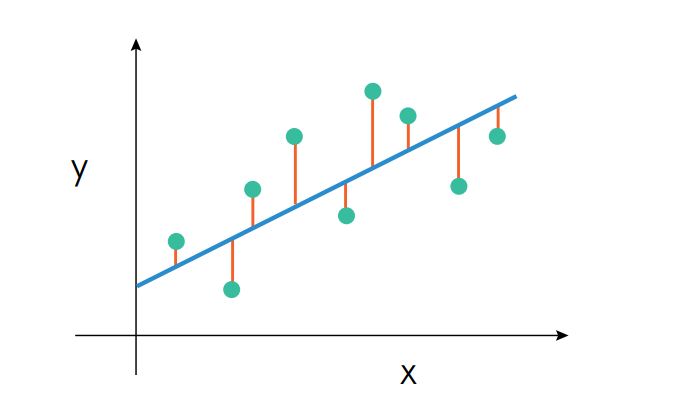
Para llevar a cabo el entrenamiento utilizamos una función matemática que permite devolver predicciones a partir de la transformación exponencial de una combinación lineal de los atributos.
![]()
Como mencionamos es un proceso iterativo, en donde cada época los coeficientes se van actualizando para acercarse al resultado deseado(separar la clase de las demás). El valor optimo de estos coeficientes son aquellos que maximizan la siguiente función objetivo(función de verosimilitud):
![]()
Ventajas:
- Simplicidad
- Fácil de interpretar las predicciones
- Tiempo de entrenamiento razonable
- Tiempo de predicción casi instantáneo
Desventajas:
- Se asume que los atributos son independientes, no tienen una correlación significativa
- Modelo muy simple, solo permite crear una línea de decisión entre dos clases
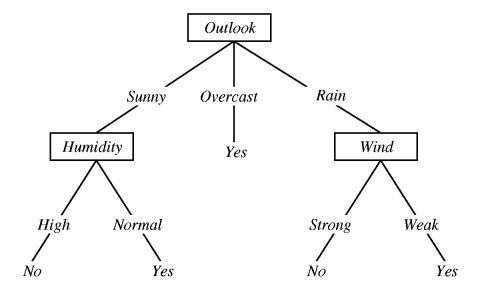
Árboles de decisión
Es un modelo de conocimiento que puede generarse a partir de datos y puede usarse tanto para clasificación como regresión. Se divide el conjunto de datos de manera jerárquica en trozos menores hasta lograr llegar a una única clase.
Antes de ver la implementación vamos a conocer el índice de Gini, veamos un ejemplo.

En este caso vamos a calcular el índice Gini por género.
![]()
![]()
![]()
![]()
![]()
![]()
Tenemos el índice de Gini para las chicas y los chicos, ahora para sacar el ponderado por genero lo que hacemos es sumar ambos índices por la frecuencia de las posibilidades.
![]()
![]()
![]()
En este caso solo lo hicimos con un atributo, pero la idea es hacerlo por todos los atributos, por ejemplo altura, edad, etc. Este valor nos sirve para detectar los atributos mas discriminativos, es decir calculamos el índice Gini para cada condición y la que tenga mas valor es la que tiene mayor rango en la jerarquía.
Ventajas:
- Simplicidad
- Fácil de interpretar las predicciones
- Tiempo de entrenamiento razonable
- Tiempo de predicción muy rápido
- Flexibilidad en la características de los datos
Desventajas:
- Riesgo de sobreajuste
- Sensibilidad al desbalanceo de las clases
Support Vector Machine(SVN)
Este algoritmo funciona a partir de funciones discriminales lineales, es decir que se limita a discriminar entre dos clases, sin embargo no significa que debamos huir a problemas multiclase, lo que hacemos es un one vs all para abordar estos problemas.
Consiste en hallar un hiperplano optimo capaz de separar el espacio muestral en dos regiones de manera que cada región pertenezca a una clase, donde el optimo es el que maximiza el margen.
A los dos puntos mas cercanos que tocan el limite del margen se les llama vectores de soporte. Definiendo un hiperplano positivo y uno negativo.
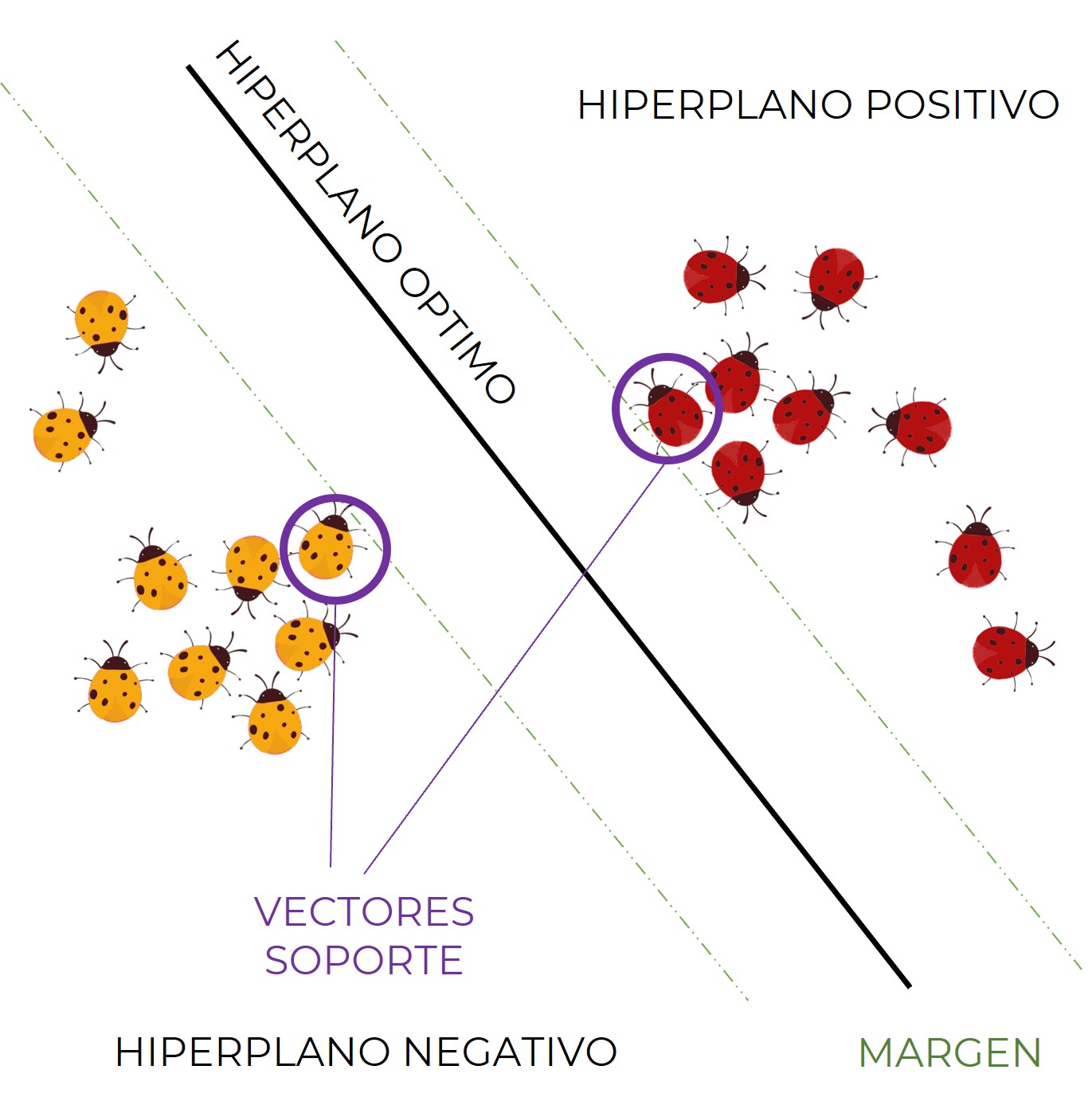
Dada una muestra ![]() y un hiperplano denotado por un vector
y un hiperplano denotado por un vector ![]() y un bias
y un bias ![]() , el objetivo es determinar la distancia de
, el objetivo es determinar la distancia de ![]() al hiperplano.
al hiperplano.
![]()
![]()
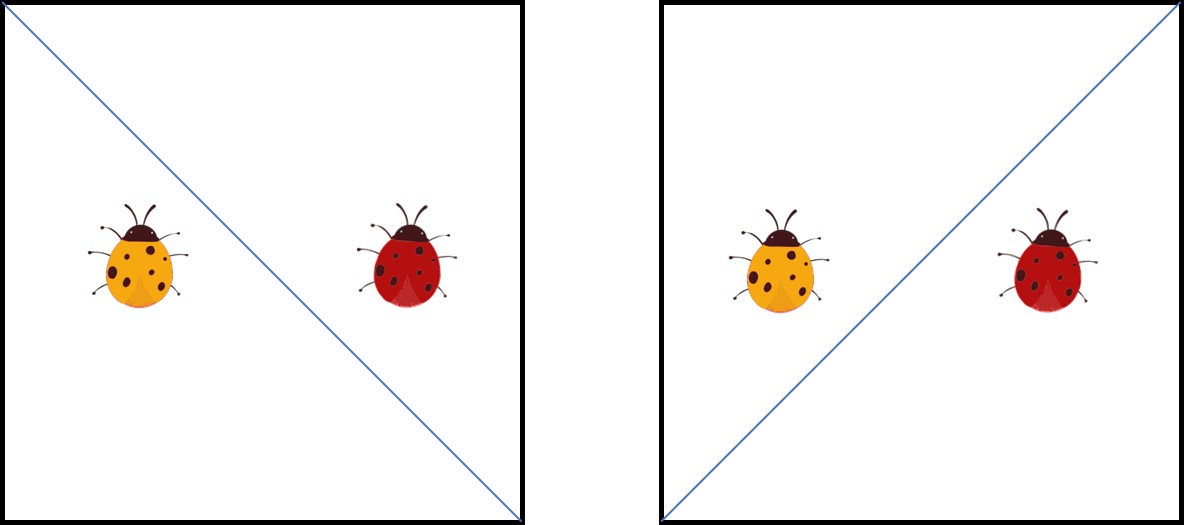
Al utilizar esta función nos encontramos con el problema del signo negativo, donde en la anterior imagen al minimizar ![]() pareciera que cualquiera de las dos opciones funciona pero solo hay un hiperplano optimo.
pareciera que cualquiera de las dos opciones funciona pero solo hay un hiperplano optimo.
Para solucionar esto se introduce la variable ![]() de manera que:
de manera que:
- Si el resultado es positivo la clasificación es correcta
- Si el resultado es negativo la clasificacion es incorrecta
Ahora el objetivo a minimizar es:
![]()
Tenemos adicionalmente otro problema, por ejemplo, un vector ![]() y
y ![]() representa el mismo hiperplano que el vector
representa el mismo hiperplano que el vector ![]() y
y ![]() . Vemos que en el caso de
. Vemos que en el caso de ![]() tenemos una
tenemos una ![]() diez veces mayor. A esto se le conoce como problema de escala. La solucion es dividir el vector
diez veces mayor. A esto se le conoce como problema de escala. La solucion es dividir el vector ![]() y el bias
y el bias ![]() , por su norma; por lo que la función objetivo a minimizar seria:
, por su norma; por lo que la función objetivo a minimizar seria:
![]()
Minimizando:
![]() donde
donde ![]()
Hasta ahora este proceso me genera un hard margin SVN que requiere que mis datos sean linealmente separables y que no haya distorcion en los datos; para solventar esto surge soft margin SVN.
El soft margin SVN introduce una variable de holgura capaz de minimizar los errores de predicción, permitiendo cometer mas errores de clasificación durante el entrenamiento, su función a minimizar es:
![]()
Donde
![]()
![]() para cualquier
para cualquier ![]()
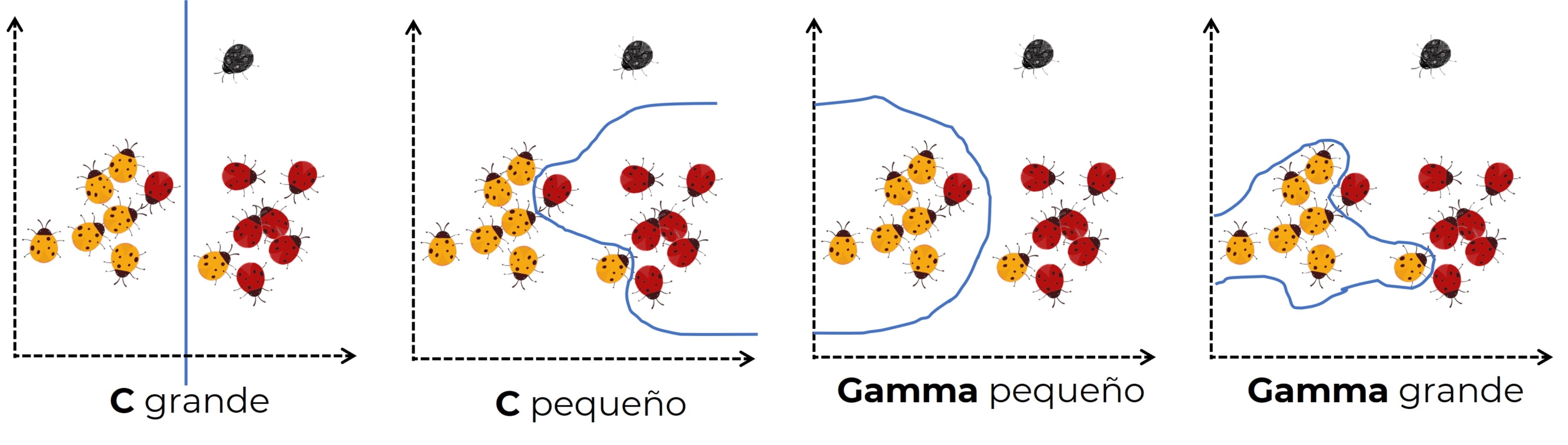
![]() (box constraint) es un parámetro de regularización que controla la compensación entre la penalización de las clasificaciones erróneas(teniendo en cuenta las variables de holgura) y el ancho del margen.
(box constraint) es un parámetro de regularización que controla la compensación entre la penalización de las clasificaciones erróneas(teniendo en cuenta las variables de holgura) y el ancho del margen.
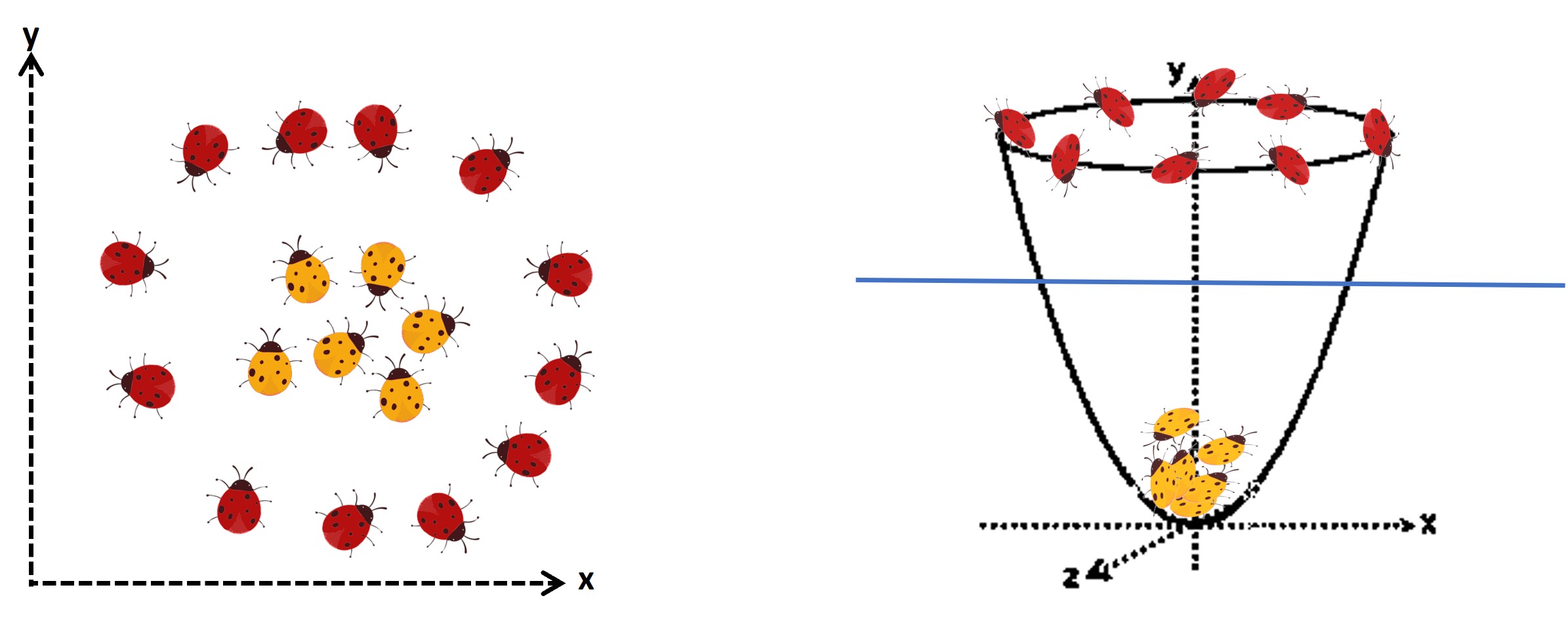
Mencionamos que se puede utilizar en datos linealmente separables, pero cuando no lo son podemos aplicar el kernel trick usando una función kernel(cuadrático, gaussiano, etc); esto permite proyectar un espacio muestral D-dimensional a otro espacio M-dimensional, donde ![]()
![]()
Esto permite separar de manera lineal aquellos datos que originalmente no eran separables.
Cuando trabajamos con kernel otro hiperparámetro que podemos usar es Gamma, se utiliza con la función RBF(radial basiss function) de kernel gaussiano. Este permite definir el grado de curvatura de la frontera de decisión. Normalmente se usan valores de gamma entre 0.01 y 100
![]()
![]()
Bagging – Bootstrap aggregating
- Divide en varios subconjuntos los datos de entrenamiento.
- Se crea un modelo(clasificador) por cada subdataset. Se puede utilizar cualquier clasificador pero el mas usado son los arboles de decisión dando el método mas conocido, random forest. Se utilizan también distinto numero de características en cada subdataset. El uso del modelo se basa en weak learners (clasificadores con al menos un 51% de éxito) para construir el strong learner
- La clasificación final se obtiene del promedio de todos los clasificadores. De esta manera este algoritmo reduce la varianza y minimiza el overfitting.
Ventajas:
- Eficiente sin ajustar hiperparámetros en problemas de clasificación y regresión
- Estabilidad y robustez en la predicción, ya que al utilizar muchos árboles prevalece el promedio de las votaciones.
- Posibilidad de utilizar gran cantidad de características
- Tiende a reducir el riesgo de overfitting.
Desventajas:
- Coste computacional más elevado que construir un solo árbol de decisión.
- Inconsistencia cuando se utilizan datasets pequeños.
BOOSTING
El entrenamiento se realiza creando también varios modelos, pero en esta ocasión lo hace en serie y en cada iteración conserva el error cometido en la anterior iteración para mejorar el modelo actual.
Aquí también se utiliza mucho los arboles de decisión como método de decisión. Y su método mas conocido es Adaboost.
- Adaboost solo se crea árboles compuestos por un solo nodo, es decir evaluá una característica y saca dos posibles predicciones, lo que se denomina stump; de esta manera, se crea lo que se conoce como Forest of Stumps. Los stumps no son buenos clasificadores por sí solos, por eso son weak learners. La idea es utilizar el stump que tenga un menor índice Gini.
-
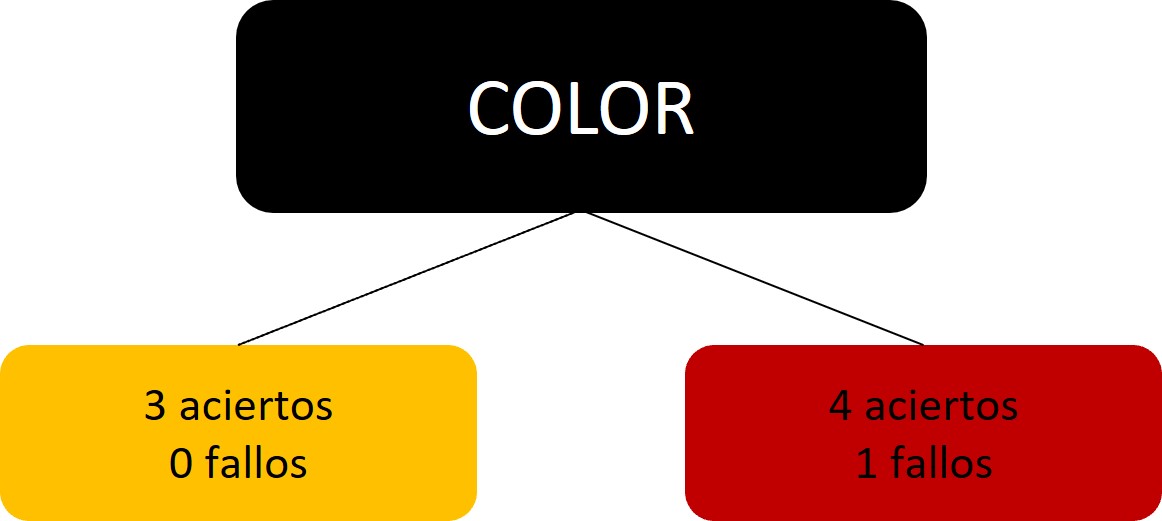
Adaboost aplica la técnica de majority voting de manera ponderada, por lo que algunos árboles contribuyen más que otros en la decisión final. Esta ponderación se hace con la siguiente ecuación:
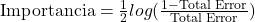
*El error es igual al número de fallos cometidos entre el total de los registros
![]()
![]()
- En los registros donde se cometen errores otorgamos mayor peso
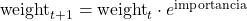
Donde no se cometen errores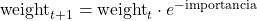
Tomando el ejemplo anterior:
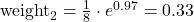 para el caso incorrecto
para el caso incorrecto
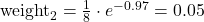 para los casos correctos
para los casos correctos - Se normalizan los pesos dividiendo cada valor entre el sumatorio de los nuevos pesos. Los pesos normalizados constituirán el nuevo sample weight.
- Se define un conjunto de datos vacío de las mismas dimensiones que el original. Después, se selecciona aleatoriamente un valor entre 0 y 1, y se añade el registro correspondiente en función de la suma ponderada de la columna de sample weight.
Ventajas:
- Fácil implementación.
- Permite corregir errores de manera iterativa usando weak classifiers.
- Mejora el rendimiento combinando weak learners.
- No produce overfitting.
Desventajas:
- Es sensible a datos ruidosos.
- Es poco robusto frente a outliers