Conceptos básicos
- Población: Conjunto del cual se quiere extraer características.
- Muestra: Subconjunto de la población. Es muy importante que este conjunto represente la población, es decir que involucre sus particularidades y características.
- Inferencia estadística: Proceso para obtener conclusiones de una población a partir de un análisis sobre una muestra.
- Variable(atributo): Representa el valor de una cualidad de una población, este valor puede variar de registro a registro.
- Ordinales: No numéricas en la que existe un criterio de orden.
- Nominales: No numérico y no admiten criterio de orden.
- Discretas: Toman un número finito de valores, son contables.
- Continuas: Toman un número infinito de valores en un rango continuo.
Análisis de variables cualitativas
Podemos usar una tabla de frecuencias para resumir y facilitar la comprensión de los datos. Esta tabla simplemente consiste en tener cada uno de los valores que puede tomar la variable y la cantidad de repeticiones(frecuencia) que hay en los datos.
Otra manera, que a mi particularmente me gusta mucho es representar el análisis por medio de gráficos de por ejemplo pie o barras(hay muchos mas). Estos permiten comprender los datos de manera muy visual y fácil, y te da una ventaja al momento de exponer sobre el tema. Tienen una facilidad tremenda de ser comprendidos y causan un impacto a nivel profesional muy bueno.
Análisis de variables cuantitativas
Podemos usar medidas de tendencia central:
Medidas de posición como en el diagrama de caja y bigotes.
Medidas de dispersión:
Medidas de distribución:
- Coeficiente de asimetría
Mide la simetría de la distribución de una variable respecto a la media aritmética
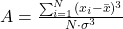
- Curtosis
Mide el grado de apuntamiento o achatamiento de la distribución de frecuencia respecto a una distribución normal
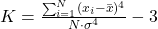

Deja un comentario